canvas 简介
在学习一项新技术之前,先了解这项技术的历史发展及成因会帮助我们更深刻的理解这项技术。
历史上,canvas 最早是由 Apple Inc. 提出的,在 Mac OS X webkit 中创建控制板组件使用,而在 canvas 称为 HTML 草案及标准之前,我们是通过一些替代方式去绘图的,比如为人所诟病的 Flash,以及非常强大的 SVG(Scalable Vector Graphics,可伸缩的矢量标记图),还有只能在 IE(IE 5.0以上的版本)中使用的 VML(Vector Markup Language,矢量可标记图)。甚至于有些前端可以使用 div+css 来完成绘图。
总的来说,没有 canvas 的时候,在浏览器绘制图形是比较复杂的,而在 canvas 出现之后,绘制 2D 图形相对变得容易了。
NOTE : 用 div 绘制一些简单的图形,如矩形,圆形,三角形,梯形,倒也算是没那么复杂。
但 canvas 也有缺点。因为 canvas 本质上是一个与分辨率相关 的位图画布 ,也就注定了在不同分辨率下,canvas绘制的内容显示的时候会有所不同。此外,canvas 绘制的内容不属于任何DOM元素 ,在浏览器的元素查看器中也找不到,那自然无法检测鼠标点击了 canvas 中的哪个内容,很显然,这两方面,canvas 都是不如 SVG 的。
举个例子 :如果使用 CSS 设置 canvas 元素的尺寸,那可能会导致绘制出来的图形变得扭曲,如长方形变正方形,圆形变椭圆等,这是因为画布尺寸和元素尺寸是不一样的,画布会自动适应元素的尺寸,如果二者是成比例的,那么画布就会等比例缩放,不会出现扭曲。
这么说来,canvas 有这么明显的缺点,那直接使用 SVG 岂不是更好?
No,听过一句话吗?没有完美的方案,只有适不适合。
SVG 是基于 XML 的,那么就说明,SVG 里面的元素都可以认为是DOM元素 ,可以启用 DOM 操作,同时,SVG 中每个绘制的图像均被视为对象,若 SVG 对象属性变化,浏览器会自动重现图形。
以上是 SVG 的优势,但通过这个优势,我们也能发现一些问题:
通常,过度使用 DOM 的应用都会变得很慢,所以,复杂的 SVG 会导致渲染速度变慢。但是像地图这类的应用,首选是 SVG。
浏览器的重排发生在浏览器窗口发生变化,元素尺寸位置变化,字体变化等等。
即使可以启用 DOM 操作,但 DOM 操作的代价还是比较昂贵的(DOM 和 JS 的实现是分开的)。
回到主题。
canvas 是通过 JavaScript 进行 2D 图形的绘制,而 <canvas> 标签本身是没有任何绘制能力的,它仅仅是一个容器。在绘制时,canvas 是逐像素的进行渲染的,一旦图形绘制完成,该元素就不再被浏览器所关注(脚本执行结束,绘制的图形也不属于DOM)。
值得注意的是,在 HTML 标准(whatwg 标准 )中明确的指出: Authors should not use the canvas element in a document when a more suitable element is available.
canvas 目前几乎被所有的浏览器支持,但是IE 9.0 之前的版本不支持 canvas元素
canvas 基本使用
canvas 是一个HTML元素,所以要使用 canvas,首先需要:
<canvas id = " canvas " width = " 600 " height = " 300 " > 当前浏览器不支持canvas </canvas> 在第一行 HTML 代码中可以看到两个属性:width 和 height ,它指明了画布的宽高,在上文中提到过,不要使用 CSS 规定尺寸,因为当 CSS 规定的尺寸和画布尺寸比例不一致时,无法成比例缩放,导致绘制出来的图形变得扭曲。在没有设置画布大小时,canvas 默认会初始化成 300px * 150px 的画布。
“当前浏览器不支持 canvas ”是元素的内容,但他只是作为一个后备内容(即 fallback content ),只有当浏览器不支持 canvas时,这个内容才会被显示出来。
canvas元素本身没有绘制能力,只是作为一个容器,所以需要通过JavaScript这类脚本进行绘制:
const canvas = document . getElementById ( ' canvas ' ) ; const context = canvas . getContext ( ' 2d ' ) ; 上面的 HTML + JS 代码是使用 canvas 所必须的,无论要绘制什么内容,这几行代码不可缺少。
getContext() 是 canvas 元素提供的方法,用于获取绘制上下文(或者说渲染上下文,The rendering context),他只有一个参数:上下文格式。这里传入 2d 表示获取 2D 图像绘制环境。由于 getContext 是 canvas 元素提供的方法,故我们可以通过检测 getContext 方法的存在性来检查浏览器的支持性。
context 变量的类型是 CanvasRenderingContext2D
渲染上下文不好理解,可以理解为画图用的笔刷。
在画布中如何确定绘制的位置?是坐标。
在 canvas 中,画布的左上角为原点,横轴为x轴表示宽,纵轴为 y轴表示高[1]
在 w3c school 中,将 canvas 提供的绘制 API 大致分为以下几种[2]
颜色、样式、阴影
线条样式
矩形
路径
转换
文本
图像绘制
像素操作
合成
其他
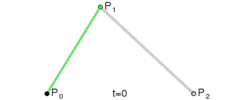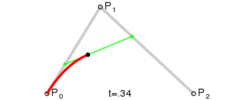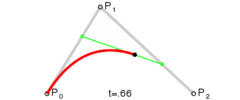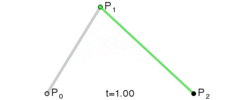
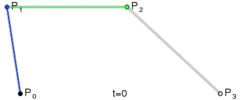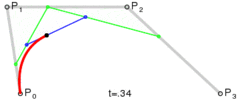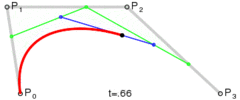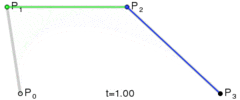
在上面这个例子中,包含了矩形,圆形,线,文字及“文字”几大块内容,细讲下去,会涉及到不少 API,会使得本文变得很长,而且没有必要,值得一提的是贝塞尔曲线,这是二维图形应用程序的数学曲线,一般的矢量图形软件就是通过它来精确画出曲线的,贝塞尔曲线是计算机图形学中相当重要的参数曲线[3]
以上图片按顺序分别是一次贝塞尔曲线,二次贝塞尔曲线,三次贝塞尔曲线。从图中,可以很清楚的看到,一次贝塞尔曲线实际上是一条直线。当然,还有更高阶次的曲线,不过canvas只提供了二次和三次贝塞尔曲线。
以二次贝塞尔曲线的API为例:
quadraticCurveTo ( cp1x , cp1y , x , y ) ; (cp1x, cp1y)表示控制点坐标,(x, y)表示结束点坐标。这里还缺少一个起始点坐标,假设是(x0, y0),那这个(x0, y0)是谁?
就是在调用 quadraticCurveTo 函数时,context(绘制上下文)所处的坐标。举个例子:
var cxt = canvas . getContext ( ' 2d ' ) ; // 认为canvas已经获取到 cxt . beginPath () ; cxt . moveTo ( 120 , 90 ) ; cxt . quadraticCurveTo ( 130 , 80 , 130 , 70 ) ; cxt . quadraticCurveTo ( 115 , 70 , 115 , 50 ) ; cxt . quadraticCurveTo ( 115 , 30 , 155 , 30 ) ; cxt . quadraticCurveTo ( 195 , 30 , 195 , 50 ) ; cxt . quadraticCurveTo ( 195 , 70 , 155 , 70 ) ; cxt . quadraticCurveTo ( 135 , 90 , 120 , 90 ) ; cxt . stroke () ; 这段代码运行结果就是一个对话框(在第一张图片中体现),可以看到,在调用二次贝塞尔曲线之前,我们设置了起点,即,将笔刷移动到坐标 (120, 90),在之后调用中,都是以前一次贝塞尔曲线的终点作为本次曲线的起点。
这时候可能会有人问:我去掉这个 moveTo 的调用是不是就画不出来了?如果后续是调用 lineTo函数,那还真就画不出来了。但是别忘了,还有一次贝塞尔曲线,这就是条直线,他是以(cp1x, cp1y)为起点,(x,y) 为终点的一条直线。所以说,去掉 moveTo 后,只会影响到第一条曲线的绘制。但是如果删除最后一行代码 stroke(),那么程序运行结束时,在浏览器上啥都看不到。
由此,我们应该思考另一个问题:为什么 stroke() 函数是必须的呢?
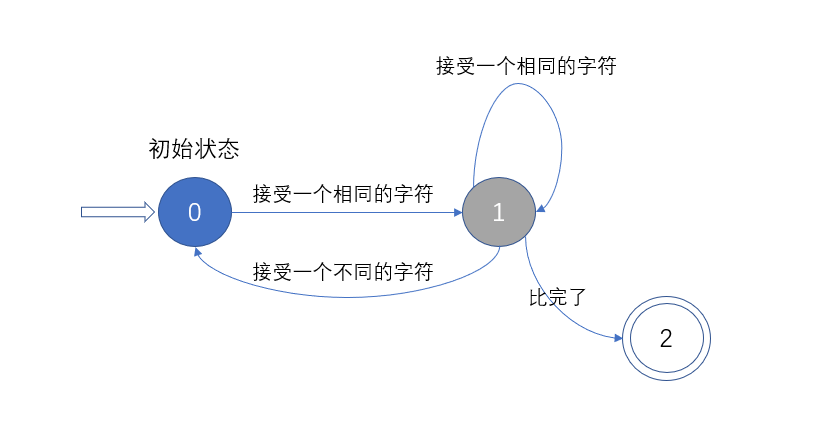
其实,canvas 是一种基于状态的绘制,依照此,可以将 canvas 提供的 API 分为两种:状态设置,具体绘制。
stroke()、fill() 等函数就是将内容绘制到 canvas 画布容器中的函数。
arc()、lineTo()、rect()等函数就是设置笔刷状态的函数。
在那种玄幻类型的电影、电视剧里面就经常能看到某个道士虚空画符,画完之后往前一推,就印在了对应的符或者人身上了。
道士虚空画符,这个过程就像是canvas设置笔刷状态的过程。
往前一推,这个就是具体的绘制了,怎么绘制咱不知道,反正这符是画上去了。(前文提到过,canvas 是逐像素渲染 的)
“文字”的绘制,注意,这个文字是打了引号的,普通文字,我们绘制只需要调用 fillText() 即可,而这里所指的文字是点阵字体 ,在单片机或者 LCD 这类程序中,通过点亮一系列的点,显示出文字或图案,点亮的过程较为复杂,可以简单的理解为 LCD 上的像素点置为1时点亮该点,为 0 时不点亮(实际可能相反)。那么 canvas 这里的“文字”绘制也是一样的道理,通过建立文字对应的字体库,当需要绘制某个文字的时候,在字体库中找到对应的文字点阵,然后将点阵中标志为 1 的位置点亮(填充)即可。
实际操作时,可能并不是点亮这么简单,你可能会想要制作出更酷的内容,用圆形去填充,用矩形去填充,甚至说想要制作出动态爆炸的效果,这时候就牵扯到一些其他的计算了。
点阵时间 上图是一个用矩形填充的示例,数字对应8×8的点阵。
canvas的高级动画
先思考一个问题,假设现在我们已经学会了绘制一个圆形的方法,现在要求做出一个和物理学相关的动画:平抛运动。
现在该如何去实现呢?
可能看到这个问题的时候,有些人瞬间懵圈了:我就学了个绘制圆的函数,你就让我模拟这么高难度的动画,你这分明是想谋害朕!
可能也有人会想到,平抛运动,在高中物理学中学到过,基本都只是研究一个小球的问题,在 2维平面中,这小球完全可以视作一个圆,可不就只需要学会画圆就行了?
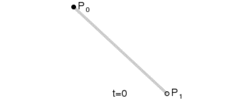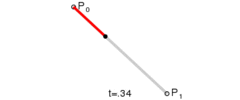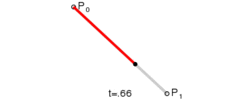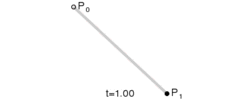
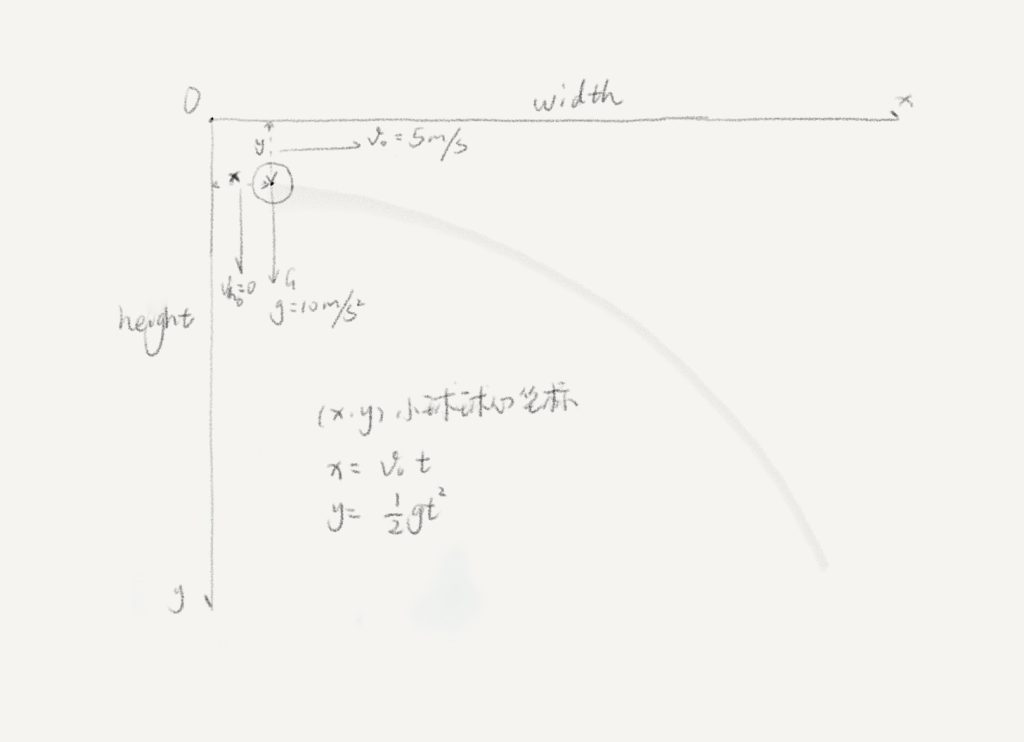
经此,我们继续往下思考,在平抛运动中的小球,假设水平方向设有初始速度 v0,除了重力外,不受到其他外力影响,也即存在一个重力加速度 g(为了计算简单,我们可以简单的设为g = 10m/s2 ),同时竖直方向没有初速度 vh(或称 vh = 0;),如下图:
平抛运动 从图中,我们可以看到一些很有意思的现象,如:小球的水平方向刚好和 canvas 画布的横轴一致,竖直方向也和纵轴方向保持一致。
然后由平抛运动对应的物理公式:
// 竖直方向无初速度,水平方向没有外力 x = v0 * t ; // 水平方向位移 h = 1 / 2 * g * t * t ; // 竖直方向位移 // 竖直方向有初速度 h = vh * t - 1 / 2 * g * t * t ; // 竖直方向位移 发现(x, h)和 canvas 上的坐标(x, y)是一致的,而且我们也不是在做物理题,也就是说,v0, t, g, vh 这些参数都是已知的,我们唯一需要做的就是,计算出任意时刻的(x, h),也即小球在 canvas 上的坐标(x, y)。
分析结束,我们现在可以得到小球在任意时刻的位置坐标,那么我们也就可以在画布上画出来任意时刻的小球。
针对上面的分析,可能会有人说:你这不对,你这个应该是具有特殊性的吧,小球未必是从左边抛出去的,从右边也可以啊,向上抛也可以。
的确,上面的分析只是取出了其中一个比较特殊的状态来研究,限于篇幅(以及本文主题是 canvas 而非物理),没有推广到更一般的结论,但其实,这些分析已经足够了,无论是位移还是速度,他都是矢量,带有方向,那么我们不妨规定:以canvas的坐标轴,数值增加的方向为正向,那么从右边抛出,可以认为是反向,可以表示为 -v0 ,最终通过计算位移的公式,可以得到正确的坐标(但这时候算坐标 x 是比较麻烦的,不能直接使用上述公式)。
分析这么多,说点儿咱最关心的实现。
在之前的分析中,我们知道想求小球任意时刻所在位置坐标,需要的参数有:v0, t, g, vh。这些参数应该存放在哪里呢?怎么设计这个数据结构?
我们当然可以直接将这些参数设为全局变量,但这显然是不合适的,这些参数里,唯一适合设为全局变量的是重力加速度 g。而v0, t, vh这些都应该是小球自身的“属性”,所以我们应该将其抽象成一个类。
function Ball ( r , v0 , vh , t ) { this . r = r ; this . v0 = v0 ; this . vh = vh ; this . t = t ; this . x = 0 ; this . h = 0 ; this . calcX = function () { /* 计算水平位移 */ } this . calcH = function () { /* 计算竖直位移 */ } } var ball = { x : 0 , h : 0 , r : 10 , v0 : 0 , vh : 0 , g : 10 } ; // 重力加速度无论是作为全局变量还是小球属性,均可 // es6之后 class Ball { constructor () ; } 以上三种方式,各有各的好处,选择一个合适的方式即可。
“你这说物理我就头大,有没有更简单的?”
更简单也有啊,反正并没有要求 100% 还原物理学场景:
var ball = { x : 0 , y : 0 , r : 10 , vx : 5 , vy : 0 , g : 5 } ; setInterval ( () => { ball . vy += ball . g ; // 竖直方向速度增加 ball . y += ball . vy ; // 竖直方向位移 ball . x += ball . vx ; // 水平方向位移 cxt . clearRect ( 0 , 0 , 800 , 300 ) ; cxt . beginPath () ; cxt . fillStyle = ' black ' ; cxt . arc ( ball . x , ball . y , ball . r , 0 , 2 * Math . PI ) ; cxt . fill () ; }, 50 ) ; OK,结束了。
这就是高级一点的动画。可能在学几个函数,这个动画会更炫一点。比如学完矩形填充再掌握一点rgba的知识,你可以做个“尾巴”出来,即长尾效应。具体只需要将上述代码中的 cxt.clearRect() 替换成:
cxt . fillStyle = ' rgba(255, 255, 255, 0.2) ' ; cxt . fillRect ( 0 , 0 , 800 , 300 ) ; 这就能显得咱们编码能力很厉害的样子。
做到这一步还是不满足:小球一个劲儿的向下掉,这动画没一会儿就没了。
没关系,咱们可以做“碰撞检测 ”啊。好像又是一个高大上的词汇,但实际上也没什么高大上的,如果基于本节第一部分的分析,那咱还得考虑一下碰撞造成的动量损失的问题,挺复杂的。
但是简化版就好说了啊。小球碰到上/下边界,竖直方向速度反向,同时速率减半。左右边界可以有类似的处理。
if ( ball . r + ball . x > canvas_width ) { ball . vx *= - 0.5 } if ( ball . r + ball . y > canvas_height ) { ball . vy *= - 0.5 ; }
NOTE:碰撞检测在这里指的是“边界检测 ”,小球落到边界的时候再继续下落显然是没有意义的,因为后面的动画咱们是看不到的。所以要么碰到边界就停止,要么重新开始,或者进行其他处理,总之,不能出现无意义的动画。
像以前玩的贪吃蛇,会有各种墙的存在,控制的小蛇在碰到墙的时候,游戏就失败了,或者说没有墙的时候,小蛇会从另一个方向出来。
小结
说了这么多,你会发现,本文不仅没有直接的罗列不同的 DEMO 来介绍函数,更是在尽量避免过多的介绍 canvas 中的API。
个人看来,canvas 其实就是一个函数库,他和我们平时使用的那些什么 forEach,splice,split,map,reduce 没什么区别,都是封装好了直接用的,查一查函数手册就可以了解用法了,多用几次就会比较熟悉了。
刚进大学的时候,专业课老师就告诉我们,程序=算法+数据结构,即使到现在,也有很多人在强调这一点。如果你有心,再回想一下上一节内容,在分析平抛运动的时候,我本质上是在考虑算法问题;在设计小球的类时,考虑了面向对象,但更多的是在考虑数据结构的问题,在考虑了这些内容的基础上,我才开始了具体的实现。
参考资料:
MDN文档 ↩︎ HTML 5 Canvas参考手册 ↩︎ 贝塞尔曲线 ↩︎